Think outside the box for the most optimal recycling solution.

Today we did some up-cycling of political ad signs. After elections these generally go in the trash, but Talent Maker City had a public event to build some cool stuff out of these corrugated plastic boards! (Update-  see the howto for version 2 of a durable cargo bicycle box here)

The first step to remaking these would be to go through the political signs and see which one seems to have the most solid political platform… ahem… I mean choose one of the signs that is not droopy or damaged or chipped.

Second, we cut along some lines on their laser-cut pattern to make a half fold in a few spots to make a plastic cell phone/tablet holder – with some adhesive velcro to make it foldable from a flat sheet to a neat little device holder!

A device holder is perhaps the most simple of the stuff they had made – there were some boxes, a tall letter-holding box… and naturally the first question on any mathematician’s mind is, how much of a volume can we make out of that plastic piece? That is, what is the biggest box we can make by cutting four identical almost-rectangular pieces from the edges and folding the four sides up?

First, I measured width and height of the sign… As you can see here the dimensions end up being these lines:

(Not to scale! In fact this is probably not the largest box you could make… let’s see…)

Here Z will be the depth of the box – in this visualization, a not very deep, very large wide box. Assuming it is done correctly by cutting out almost a square – with some room for overlap and attaching side together, what is the volume? x*y*z.

The problem is, we have constraints on this – that is, it cannot be any x,y,z that we want. When we know the width of the box is 61.3cm wide, and 45.7cm tall, you can see by the diagram above that means

61.3 = y+z+z

45.7 = x+z+z

Oh no, there are still three variables and there aught to be one variable to make it simpler… Notice that those equations give one variable in terms of another so we want to find replacements so that the volume formula x*y*z doesn’t have three different things to try and optimize! Note that both of those have a 2*z in them, and we can do some algebra to get an equivalent with only one variable:

From the two equations above we can say:

2z = 61.3 – y

2z = 45.7 – x

and equivalently, 61.3-y = 45.7-x. From this we can say -y = -15.6-x, or equivalently y = 15.6+x.

Z = ½ *(45.7-x) so we now have replacements for y and z to make the entire x*y*z volume formula all in terms of x.

Volume of box = x*y*z = x*(15.6+x)*(22.85-.5x) with the above replacements.

Volume = (x²+15.6x) * (-.5x+22.85)

Volume = -.5x³ + 22.85x² -7.8x² +356.46x

You can verify on a plot that there’s 0 volume on a theoretical 0-height box and there is 0 volume to a box that has no sides… that is x=45.7. So this function looks good so far:

I think it’s a sign we need calculus…

It should be easy to see the approximate peak volume on that chart, but Calculus can give the exact answer. Think back to Calculus and remember how you solve for derivative zero – dig up the ol’ calculus book or have a quick review online.

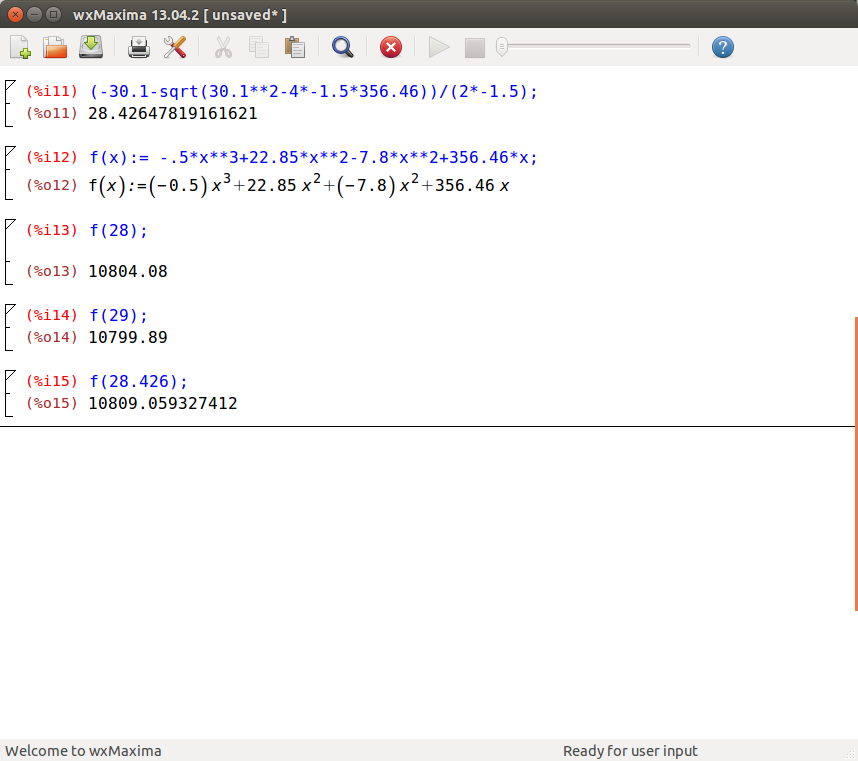
Now for the above function the derivative is -1.5x²+30.1x+356.46

Recall that the derivative of a function is zero at a “peak” or “valley”, and to solve the exact high point on the graph, you can solve 0=-1.5x²+30.1x+356.46 using complete the square or the quadratic formula.

You will come up with two values, one of which is negative which doesn’t work. The correct answer is 28.426cm and you can verify that the volume function with x less than or more than this value is slightly less!

Too much calculus? Not to worry….

I know what you may be thinking… I want machine-learning methods to solve this, what if I don’t have time to dig up the calculus book? Well, there is a solution to this calling Newton’s method, a handy method that is programmed into SciPy. We know we want the maximum (the zero derivative) of the function, we can actually have SciPy calculate this in a few lines of code with numerical methods:

#https://docs.scipy.org/doc/scipy/reference/generated/scipy.misc.derivative.html
from scipy.misc import derivative
#https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.newton.html
from scipy.optimize import newton

def f(x):
	#Note ** is power symbol in Python
	return -.5*x**3+22.85*x**2-7.8*x**2+356.46*x

def derivF(x):
	return derivative(f,x) #Derivative of function f, at x.

#Lucky guess 2?
root = newton(derivF, 2)
print( "Root is %s" % (root,))

#No no that is negative. Try with another initial guess:
root = newton(derivF, 20)
print( "Root is %s" % (root,))

Note that it still helps to know how calculus works, it could be confusing to get a negative value unless you remember that the derivative of a cubic is a quadratic function, and the quadratic has two solutions. Newton’s method is a very fast way to find the zero (root) of a function starting with a guess, and as long as we consider it may not be the only zero of the function, we can get good numerical results.
Final note
As you may have noted, most tape measures have inches not centimeters, if so you can use the following values for inches:
X=11.19in
Y=17.33in
z=3.4in