Thousands of years ago, probably around the invention of the wheel, and before the time of Solomon, humans must have been measuring various objects… calculating some distances, and wondering, is there a better way to measure how far around the outside of a wheel is compared to its diameter? Perhaps they tried for various sizes, small pebbles, small wheels… large wheels… to try and see a pattern that makes it not necessary to measure off a very long string every time to get a circumference?

Thankfully this is an easy function to figure out, for each measured radius and circumference around the circle, circumference is 3.14159… times the diameter, and the function here is linear.
Let’s make a neural network to recreate this “aha” moment and discovery of pi using machine learning. First let’s get a simple input and expected output array to run with a neural network:
from keras.models import Sequential from keras.layers import Dense import numpy as np import math model = Sequential() model.add(Dense(1, activation='softmax',input_dim=1)) train_x = np.array(range(250)) train_y = np.array([x*math.pi for x in train_x]) print(train_y)
As you may know, machine learning runs well with a whole bunch of data. Here we give an exact value of what robot-brain would measure if it were physically reading measurements for these various round objects with diameter 0 through 249. You will see…
[ 0. 3.14159265 6.28318531 9.42477796 12.56637061 15.70796327 18.84955592 21.99114858 25.13274123 28.27433388 31.41592654 34.55751919 37.69911184 40.8407045 43.98229715 47.1238898 50.26548246 53.40707511 56.54866776 59.69026042 62.83185307 65.97344573 69.11503838 72.25663103 75.39822369 78.53981634 81.68140899 84.82300165 87.9645943 91.10618695 94.24777961 97.38937226 100.53096491 103.67255757 106.81415022 109.95574288 113.09733553 116.23892818 119.38052084 122.52211349 ...
Now let’s give a very very simple robot-brain the inputs [0,1,2,3…] and try to get it to find the relation to the expected outputs…
model.compile(loss='mse',optimizer='adam', metrics=['accuracy'])
model.fit(train_x, train_y, epochs=700, batch_size=100)
model.save("pi.hdf")
for diameter in train_x:
prediction = model.predict( np.array([diameter]))
print( '%s:%s, computer thinks pi is %s' % ( diameter, prediction, prediction/diameter ))
This generates a model for the problem, saves it to file (this step is completely optional) and gives the prediction for each x diameter.
Run this code, and… oops, there is a problem. It is giving a “1 circumference” result for each value.
... Epoch 693/700 250/250 [==============================] - 0s 16us/step - loss: 203603.4469 - acc: 0.0000e+00 Epoch 694/700 250/250 [==============================] - 0s 11us/step - loss: 203603.4562 - acc: 0.0000e+00 Epoch 695/700 250/250 [==============================] - 0s 9us/step - loss: 203603.4438 - acc: 0.0000e+00 Epoch 696/700 250/250 [==============================] - 0s 8us/step - loss: 203603.4469 - acc: 0.0000e+00 Epoch 697/700 250/250 [==============================] - 0s 8us/step - loss: 203603.4500 - acc: 0.0000e+00 Epoch 698/700 250/250 [==============================] - 0s 12us/step - loss: 203603.4562 - acc: 0.0000e+00 Epoch 699/700 250/250 [==============================] - 0s 10us/step - loss: 203603.4469 - acc: 0.0000e+00 Epoch 700/700 250/250 [==============================] - 0s 10us/step - loss: 203603.4469 - acc: 0.0000e+00 ./nnpi.py:19: RuntimeWarning: divide by zero encountered in true_divide print( '%s:%s, computer thinks pi is %s' % ( diameter, prediction, prediction/diameter )) 0:[[ 1.]], computer thinks pi is [[ inf]] 1:[[ 1.]], computer thinks pi is [[ 1.]] 2:[[ 1.]], computer thinks pi is [[ 0.5]] 3:[[ 1.]], computer thinks pi is [[ 0.33333334]] 4:[[ 1.]], computer thinks pi is [[ 0.25]] 5:[[ 1.]], computer thinks pi is [[ 0.2]] 6:[[ 1.]], computer thinks pi is [[ 0.16666667]] 7:[[ 1.]], computer thinks pi is [[ 0.14285715]] 8:[[ 1.]], computer thinks pi is [[ 0.125]] 9:[[ 1.]], computer thinks pi is [[ 0.11111111]] 10:[[ 1.]], computer thinks pi is [[ 0.1]] 11:[[ 1.]], computer thinks pi is [[ 0.09090909]] 12:[[ 1.]], computer thinks pi is [[ 0.08333334]] 13:[[ 1.]], computer thinks pi is [[ 0.07692308]] 14:[[ 1.]], computer thinks pi is [[ 0.07142857]] ...
It turns out the softmax function is for multiple inputs coming in… in fact the docs say it should throw an error for just one input??
Let’s try a linear activation for this function and see what it does…
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
import math
model = Sequential()
model.add(Dense(1, activation='linear',input_dim=1))
train_x = np.array(range(250))
train_y = np.array([x*math.pi for x in train_x])
print(train_y)
model.compile(loss='mse',optimizer='adam', metrics=['accuracy'])
model.fit(train_x, train_y, epochs=700, batch_size=100)
model.save("pi.hdf")
for diameter in train_x:
prediction = model.predict( np.array([diameter]))
print( '%s:%s, computer thinks pi is %s' % ( diameter, prediction, prediction/diameter ))
And the output is:
... 250/250 [==============================] - 0s 10us/step - loss: 7385.4433 - acc: 0.0000e+00 Epoch 688/700 250/250 [==============================] - 0s 12us/step - loss: 7346.4989 - acc: 0.0000e+00 Epoch 689/700 250/250 [==============================] - 0s 10us/step - loss: 7307.1777 - acc: 0.0000e+00 Epoch 690/700 250/250 [==============================] - 0s 11us/step - loss: 7270.0424 - acc: 0.0000e+00 Epoch 691/700 250/250 [==============================] - 0s 8us/step - loss: 7230.2705 - acc: 0.0000e+00 Epoch 692/700 250/250 [==============================] - 0s 8us/step - loss: 7191.8240 - acc: 0.0000e+00 Epoch 693/700 250/250 [==============================] - 0s 7us/step - loss: 7152.7945 - acc: 0.0000e+00 Epoch 694/700 250/250 [==============================] - 0s 7us/step - loss: 7114.3938 - acc: 0.0000e+00 Epoch 695/700 250/250 [==============================] - 0s 8us/step - loss: 7076.5807 - acc: 0.0000e+00 Epoch 696/700 250/250 [==============================] - 0s 8us/step - loss: 7036.8849 - acc: 0.0000e+00 Epoch 697/700 250/250 [==============================] - 0s 7us/step - loss: 6998.8652 - acc: 0.0000e+00 Epoch 698/700 250/250 [==============================] - 0s 7us/step - loss: 6961.6289 - acc: 0.0000e+00 Epoch 699/700 250/250 [==============================] - 0s 18us/step - loss: 6922.9076 - acc: 0.0000e+00 Epoch 700/700 250/250 [==============================] - 0s 15us/step - loss: 6886.2189 - acc: 0.0000e+00 ./nnpi.py:19: RuntimeWarning: divide by zero encountered in true_divide print( '%s:%s, computer thinks pi is %s' % ( diameter, prediction, prediction/diameter )) 0:[[ 1.60629654]], computer thinks pi is [[ inf]] 1:[[ 4.16281796]], computer thinks pi is [[ 4.16281796]] 2:[[ 6.71933937]], computer thinks pi is [[ 3.35966969]] 3:[[ 9.27586079]], computer thinks pi is [[ 3.09195352]] 4:[[ 11.8323822]], computer thinks pi is [[ 2.95809555]] 5:[[ 14.38890362]], computer thinks pi is [[ 2.87778068]] 6:[[ 16.94542503]], computer thinks pi is [[ 2.82423759]] 7:[[ 19.5019455]], computer thinks pi is [[ 2.78599215]] 8:[[ 22.05846786]], computer thinks pi is [[ 2.75730848]] 9:[[ 24.61499023]], computer thinks pi is [[ 2.73499894]] 10:[[ 27.1715107]], computer thinks pi is [[ 2.71715117]] 11:[[ 29.72803116]], computer thinks pi is [[ 2.70254827]] 12:[[ 32.28455353]], computer thinks pi is [[ 2.69037938]] 13:[[ 34.8410759]], computer thinks pi is [[ 2.6800828]] 14:[[ 37.39759445]], computer thinks pi is [[ 2.67125678]] 15:[[ 39.95411682]], computer thinks pi is [[ 2.66360784]] 16:[[ 42.51063919]], computer thinks pi is [[ 2.65691495]] 17:[[ 45.06716156]], computer thinks pi is [[ 2.65100956]] 18:[[ 47.62368393]], computer thinks pi is [[ 2.6457603]] 19:[[ 50.18020248]], computer thinks pi is [[ 2.64106321]] 20:[[ 52.73672485]], computer thinks pi is [[ 2.63683629]] 21:[[ 55.29324722]], computer thinks pi is [[ 2.63301182]] 22:[[ 57.84976578]], computer thinks pi is [[ 2.62953472]] 23:[[ 60.40628815]], computer thinks pi is [[ 2.62636042]] 24:[[ 62.96281052]], computer thinks pi is [[ 2.62345052]] ...
Now this is getting somewhere! Since the loss is getting smaller and smaller, give it more epochs training time – let’s try “epochs=7000″…
With this change you should get….
... Epoch 6989/7000 250/250 [==============================] - 0s 11us/step - loss: 8.6996e-10 - acc: 0.0040 Epoch 6990/7000 250/250 [==============================] - 0s 9us/step - loss: 1.1100e-09 - acc: 0.0040 Epoch 6991/7000 250/250 [==============================] - 0s 10us/step - loss: 2.0296e-09 - acc: 0.0040 Epoch 6992/7000 250/250 [==============================] - 0s 10us/step - loss: 1.3331e-09 - acc: 0.0040 Epoch 6993/7000 250/250 [==============================] - 0s 9us/step - loss: 1.9024e-09 - acc: 0.0040 Epoch 6994/7000 250/250 [==============================] - 0s 8us/step - loss: 2.9781e-09 - acc: 0.0040 Epoch 6995/7000 250/250 [==============================] - 0s 8us/step - loss: 1.8108e-09 - acc: 0.0040 Epoch 6996/7000 250/250 [==============================] - 0s 8us/step - loss: 8.5055e-10 - acc: 0.0040 Epoch 6997/7000 250/250 [==============================] - 0s 8us/step - loss: 8.8337e-10 - acc: 0.0040 Epoch 6998/7000 250/250 [==============================] - 0s 8us/step - loss: 6.0212e-10 - acc: 0.0040 Epoch 6999/7000 250/250 [==============================] - 0s 8us/step - loss: 5.9753e-10 - acc: 0.0040 Epoch 7000/7000 250/250 [==============================] - 0s 8us/step - loss: 8.7943e-10 - acc: 0.0040 ./nnpi.py:19: RuntimeWarning: divide by zero encountered in true_divide print( '%s:%s, computer thinks pi is %s' % ( diameter, prediction, prediction/diameter )) 0:[[ 1.26110535e-05]], computer thinks pi is [[ inf]] 1:[[ 3.14160514]], computer thinks pi is [[ 3.14160514]] 2:[[ 6.2831974]], computer thinks pi is [[ 3.1415987]] 3:[[ 9.42479038]], computer thinks pi is [[ 3.14159679]] 4:[[ 12.56638241]], computer thinks pi is [[ 3.1415956]] 5:[[ 15.70797443]], computer thinks pi is [[ 3.14159489]] 6:[[ 18.84956932]], computer thinks pi is [[ 3.14159489]] 7:[[ 21.99116135]], computer thinks pi is [[ 3.14159441]] 8:[[ 25.13275337]], computer thinks pi is [[ 3.14159417]] 9:[[ 28.2743454]], computer thinks pi is [[ 3.14159393]] 10:[[ 31.41593742]], computer thinks pi is [[ 3.14159369]] 11:[[ 34.55752945]], computer thinks pi is [[ 3.14159369]] 12:[[ 37.69912338]], computer thinks pi is [[ 3.14159369]] 13:[[ 40.8407135]], computer thinks pi is [[ 3.14159346]] 14:[[ 43.98230743]], computer thinks pi is [[ 3.14159346]] ...
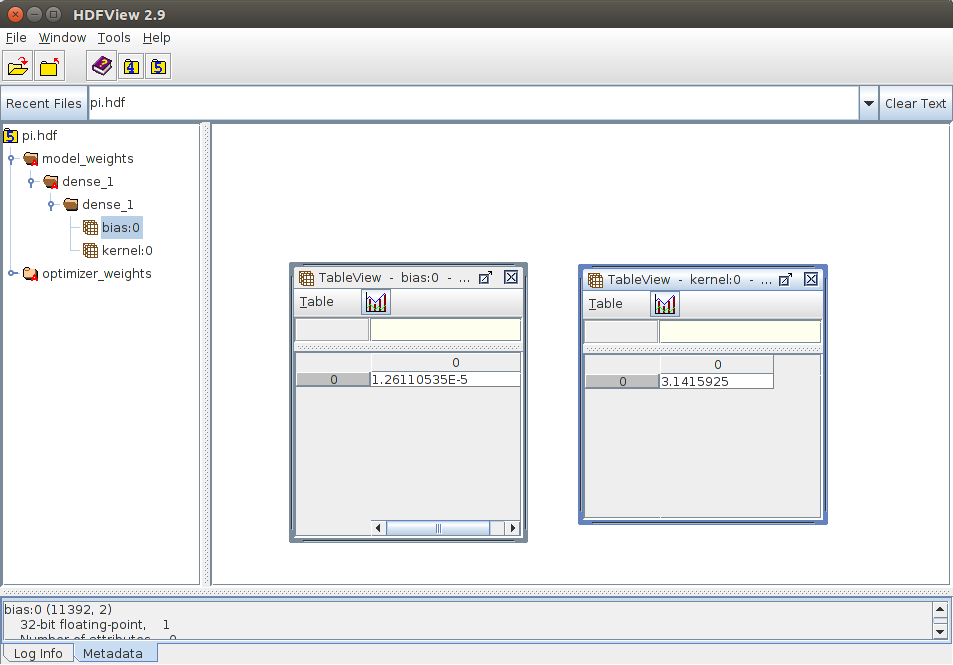
Congratulations! this concludes the most ridiculous (ridiculously simple) neural network! If you read the generated hdf file in hdfview, you can see the bias added should be super close to zero, and the matrix just has one multiplication, by approximately pi: